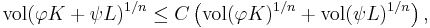Milman's reverse Brunn–Minkowski inequality
In mathematics, Milman's reverse Brunn-Minkowski inequality is a result due to Vitali Milman that provides a reverse inequality to the famous Brunn-Minkowski inequality for convex bodies in n-dimensional Euclidean space Rn. At first sight, such a reverse inequality seems to be impossible, since if K and L are convex bodies with unit volume, the volume of their Minkowski sum K + L can be arbitrarily large. However, the use of volume-preserving linear maps allows one to prove Milman's reverse inequality, similarly to the reverse isoperimetric inequality. The result is also important in the local theory of Banach spaces.
Statement of the inequality
There is a constant C, independent of n, such that for any two centrally symmetric convex bodies K and L in Rn, there are volume-preserving linear maps φ and ψ from Rn to itself such that
where vol denotes n-dimensional Lebesgue measure and the + on the left-hand side denotes Minkowski addition.
References
- Gardner, Richard J. (2002). "The Brunn-Minkowski inequality". Bull. Amer. Math. Soc. (N.S.) 39 (3): pp. 355–405 (electronic). doi:10.1090/S0273-0979-02-00941-2. http://www.ams.org/bull/2002-39-03/S0273-0979-02-00941-2/S0273-0979-02-00941-2.pdf.
- Milman, Vitali D. and Schechtman, Gideon (1986). Asymptotic theory of finite-dimensional normed spaces. Volume 1200 in Lecture Notes in Mathematics. Berlin: Springer-Verlag. pp. pp. viii+156. ISBN 3-540-16769-2.